Support Vector Machines: A Comprehensive Guide
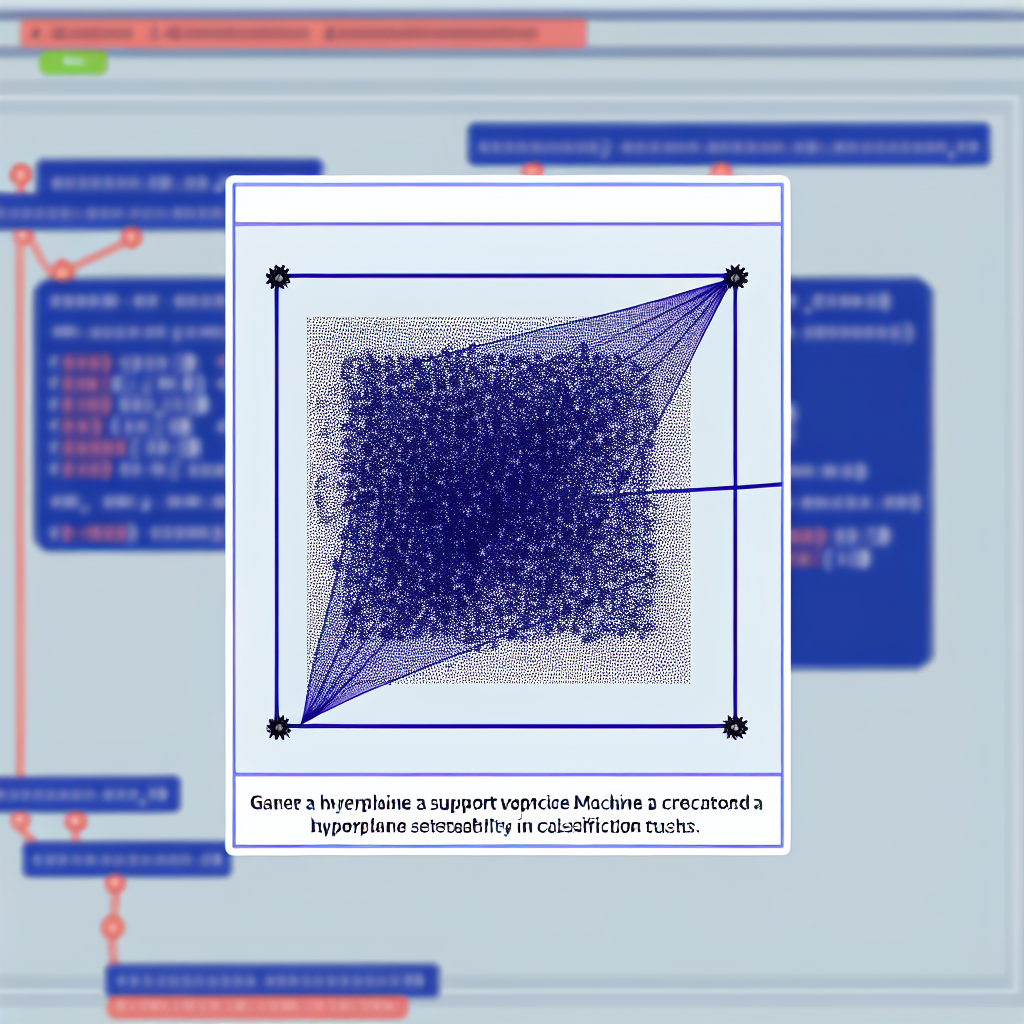
Table of Contents
Introduction to Support Vector Machines
Support Vector Machines (SVMs) are a powerful set of supervised learning algorithms used for classification and regression tasks in the field of machine learning. Developed in the 1990s, SVMs have become a staple in the toolkit of data scientists and machine learning practitioners due to their robustness and versatility. The primary goal of an SVM is to find the optimal hyperplane that separates data points of different classes in a high-dimensional space. This hyperplane maximizes the margin between the closest data points of each class, known as support vectors, which is critical for the algorithm’s generalization to unseen data.
Understanding the Mechanics
The mechanics of SVMs revolve around the concept of finding the hyperplane that best divides a dataset into distinct classes. In a two-dimensional space, this hyperplane is a line, but in higher dimensions, it becomes a plane or a hyperplane. The SVM algorithm works by transforming the original data into a higher-dimensional space, where it becomes easier to separate the data linearly. This transformation is achieved through kernel functions, which play a crucial role in SVM’s ability to handle non-linearly separable data. Commonly used kernels include linear, polynomial, radial basis function (RBF), and sigmoid kernels. The choice of kernel can significantly affect the performance of an SVM model, making it a critical step in the model design process.
Applications of Support Vector Machines
Support Vector Machines have found applications in various domains due to their effectiveness in classification tasks. In the field of bioinformatics, SVMs are used for protein classification and gene expression analysis. In finance, they help in credit scoring and risk management. SVMs are also employed in image classification, text categorization, and handwriting recognition. One of the key advantages of SVMs is their ability to handle high-dimensional data, making them suitable for tasks involving complex datasets with many features. Additionally, SVMs are known for their robustness in scenarios where the number of dimensions exceeds the number of samples, a common occurrence in real-world applications.
Advantages and Limitations
The advantages of Support Vector Machines include their ability to achieve high accuracy with less overfitting, especially in high-dimensional spaces. SVMs are versatile, with various kernel functions allowing them to fit the model to the data effectively. They perform well in binary classification tasks and are relatively memory efficient. However, SVMs also have limitations. They can be computationally expensive, particularly in large datasets, as the algorithm requires solving a quadratic optimization problem. Additionally, SVMs are not well-suited for datasets with a large number of outliers or noise, as these can significantly affect the placement of the hyperplane. Selecting the appropriate kernel and tuning hyperparameters can also be challenging and time-consuming.
Impact on Machine Learning
Support Vector Machines have had a profound impact on the field of machine learning, influencing both academic research and practical applications. Their introduction marked a significant advancement in classification algorithms, providing a robust alternative to neural networks and decision trees, which were prevalent at the time. SVMs have driven the development of new techniques and inspired improvements in kernel methods and optimization strategies. They have also contributed to the growth of interest in machine learning, as their success in various competitions and benchmarks demonstrated their practical utility and effectiveness. Today, SVMs continue to be a valuable tool in the machine learning arsenal, often used as a benchmark for evaluating new algorithms and approaches.
Conclusion
In conclusion, Support Vector Machines remain a cornerstone of machine learning, known for their ability to tackle complex classification problems with high precision. Their mathematical foundation, combined with the flexibility offered by kernel methods, allows them to handle a diverse range of tasks. Despite some limitations, such as computational cost and sensitivity to outliers, SVMs continue to be favored for their accuracy and efficiency in high-dimensional spaces. As machine learning evolves, SVMs are likely to remain relevant, adapting to new challenges and contributing to the advancement of the field.