Understanding Support Vector Machines: A Detailed Exploration
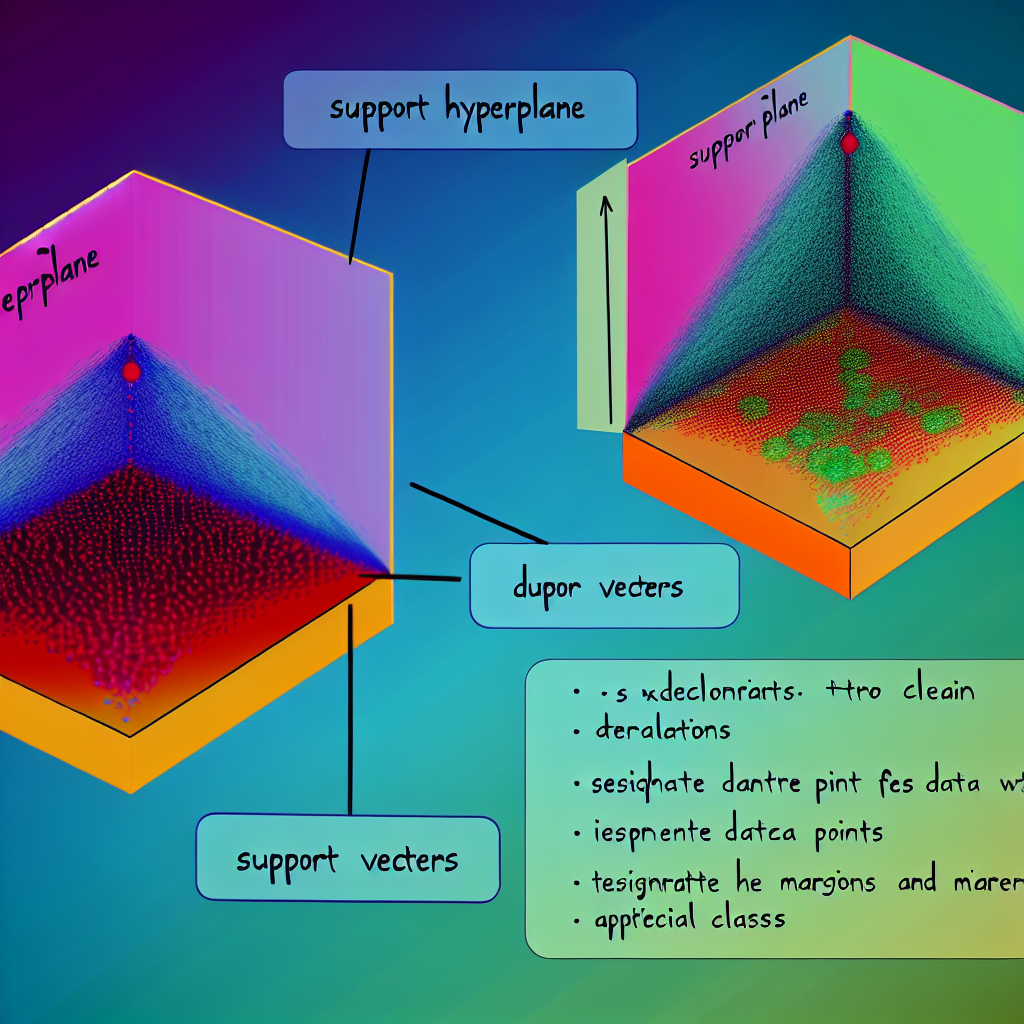
Table of Contents
Introduction to Support Vector Machines
Support Vector Machines (SVM) are a powerful set of supervised learning algorithms used for classification and regression tasks. They are particularly popular in the field of machine learning due to their ability to handle high-dimensional data and their effectiveness in scenarios where the number of dimensions exceeds the number of samples. SVMs are primarily used for classification problems, where the goal is to assign labels to instances based on their attributes. The concept of SVMs was introduced in the 1960s, and they gained significant attention in the 1990s with the development of the kernel trick, which allows them to perform in a non-linear classification space.
The Core Concept of SVMs
At the heart of Support Vector Machines is the idea of finding the optimal hyperplane that best separates the data into different classes. In a two-dimensional space, this hyperplane is simply a line, but in higher dimensions, it becomes a flat subspace. The optimal hyperplane is the one that maximizes the margin between the two classes, ensuring that the distance between the closest points of each class, known as support vectors, is as large as possible. This maximization of the margin is crucial because it provides a greater buffer zone between classes, which helps improve the model’s ability to generalize to new data.
Kernel Trick and Non-linear SVMs
One of the most compelling features of SVMs is their ability to perform classification in a non-linear space using the kernel trick. The kernel trick involves transforming the original data into a higher-dimensional space where a linear separation is possible. This is done using kernel functions, which calculate the inner products of the data in this transformed space without explicitly computing the coordinates. Popular kernel functions include the linear, polynomial, radial basis function (RBF), and sigmoid kernels. By using these kernels, SVMs can model complex, non-linear decision boundaries, making them highly versatile for various classification tasks.
Applications of Support Vector Machines
Support Vector Machines have a wide range of applications across different domains. In the field of bioinformatics, SVMs are used for protein classification and cancer diagnosis based on gene expression data. In the finance sector, they are applied to credit scoring and stock market prediction. SVMs are also employed in image and handwriting recognition, where they help in distinguishing between different objects or characters. Their ability to handle large feature spaces makes them particularly useful in text categorization and sentiment analysis, where each word or phrase can be considered a feature. The versatility and robustness of SVMs make them a go-to choice for many machine learning practitioners.
Advantages and Limitations
Support Vector Machines offer several advantages, such as their effectiveness in high-dimensional spaces and their ability to work well with clear margin separation. They are also memory efficient, as they use a subset of training points in the decision function. However, SVMs also have some limitations. They can be less effective when the data set has a lot of noise, overlapping classes, or when the number of features is much greater than the number of samples. Additionally, choosing the right kernel and tuning the hyperparameters can be challenging and requires a good understanding of the problem domain.
Conclusion
In conclusion, Support Vector Machines are a powerful tool in the machine learning arsenal, known for their ability to handle complex classification tasks with high accuracy. Their reliance on maximizing the margin between classes makes them particularly adept at generalizing to new data. While they have their limitations, particularly in terms of computational cost and sensitivity to noise, their strengths often outweigh these drawbacks in many practical applications. As machine learning continues to evolve, SVMs remain a valuable technique for researchers and practitioners alike, especially when dealing with high-dimensional data or when a clear decision boundary is required.